5° Grado - Fracciones (parte 2)

 ESCUELA N°22 D.E.E 13 "SANTA MARÍA DE LOS BUENOS AIRES"

5° GRADO - TURNO MAÑANA

ACTIVIDADES DE MATEMÁTICAS

FRACCIONES (PARTE 2)

En la entrada anterior, conocimos sobre qué era una fracción, para qué servía, como se leían, algunos tipos de fracciones... un montón de cosas. También aprendimos que las fracciones pertenecen a lo que llamamos NÚMEROS RACIONALES, y que este nombre proviene de RACIÓN, o sea, de partir.

Hoy vamos a recuperar algo que la historieta de Pitágoras mencionó y tiene que ver con ampliar o reducir fracciones.

Uno de los conceptos que les tienen que quedar en claro es que aunque se expresen de diferentes maneras, hay fracciones que representan al mismo número. (recuerden esto que aparece en negrita porque lo vamos a retomar más adelante), Veamos algunos ejemplos:

Si observás este gráfico, verás que la parte "pintada" en cada caso es la misma, por eso decimos que 1/2, 2/4 y 4/8 son fracciones equivalentes, porque equivalen a la misma cantidad. 

Aqui te dejo algunos otros ejemplos:

¿Cómo se construye una fracción equivalente?

Si observás con atención, hay algo que hace que el númerador y el denominador aumenten en la misma proporción, o dicho de otra manera, se agranden al mismo "ritmo". 

Pensemos en 1/2

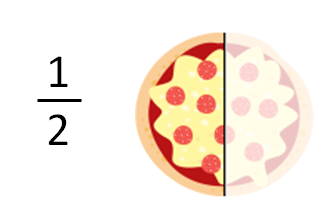
Aquí vemos una pizza dividida a la mitad, donde cada parte es media pizza (1/2). Si a cada una de las partes la dividimos a la mitad, vamos a obtener que tenemos el doble de partes (teníamos 2 y ahora vamos a tener 4), y lo representado a su vez va a pasar de 1 parte a 2 partes (de 1/2 a 2/4).

Pensar en el doble de algo...¿no es lo mismo que multiplicarlo por 2?

Mirá el dibujo que sigue:

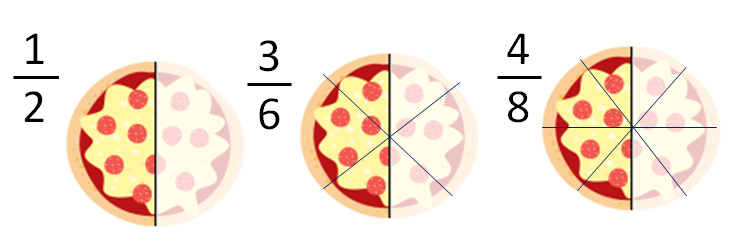
En este dibujo se puede observar que cada mitad de pizza se dividió de una forma diferente. Respondé en tu carpeta: 

• ¿En cuántas partes se dividió cada 1/2 en los diferentes gráficos?
• ¿Por qué número debería multiplicarse el numerador para pasar de 1/2 a 4/8? ¿Y el denominador?
• A un niño que estaba aprendiendo este tema se le ocurrió que para hacer fracciones equivalentes bastaba con multiplicar el numerador por un número cualquiera. ¿Estás de acuerdo con esta afirmación? ¿Por qué? Justificá tu respuesta.

Esto que venimos viendo hasta acá presentó casos de fracciones cuyo numerador y denominador se fue aumentando. Estuvimos amplificando fracciones. Pero también lo podemos pensar de la manera inversa y en lugar de dividir las partes podemos juntarlas. Mirá el siguiente gráfico:

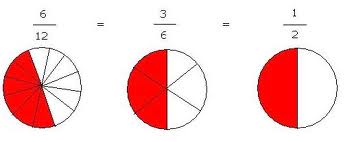
En estos casos, pasamos de fracciones con numeradores y denominadores mayores a otros con numeradores y denominadores menores, pero la parte representada sigue siendo la misma. Por eso no importa si repartimos en más partes o si las juntamos en menos, las fracciones siguen siendo equivalentes. En este caso estamos reduciendo fracciones.

Analizá estos gráficos y respondé en tu carpeta:

• Pensá algún procedimiento para escribir reducir fracciones. Explicálo para que podamos compararlos con los de otros compañeros
• El mismo alumno que te conté antes, me dijo que para hacer reducciones alcanza con dividir el númerador y el denominador por cualquier número, siempre y cuando se divida a ambos por el mismo número. ¿Estás de acuerdo con lo que dijo? ¿Por qué? Justifica tu respuesta.

Ejercitación

Te dejo algunos ejercicios para ir practicando lo que aprendimos hasta ahora.

1) Completá los cuadrados y escribí que cuenta hiciste para determinar el número que escribiste en cada caso.

2) Reducí cada fracción anotando la cuenta que tuviste que hacer en cada caso.

3) ¿Qué método usaste para elegir el número que ibas a aplicar para cada reducción? Explicalo para que podamos compararlos con los de otros compañeros.

¡Uf! ¡Cuánto que trabajamos hoy! Estoy orgullosa de ustedes. Junten pilas porque mañana vamos a aprender un poco más sobre fracciones y se viene un juego muy divertido con estos números. 

Nos encontramos mañana. Un beso de tiza.

La Seño Andrea.